Second Analysis
When you point to the number one, you are actually pointing to something that exists.
The question is "how wide is the “number 1" you’re pointing at?"
- ... Of course the number 1 is the area of 0 to 0.999999999999999 ...
- ...Similarly the number 2 is
area from 0 to 1.999999999999999 ...
It can be seen here that even from the left side there are connecting points as decimal numbers to the set of real numbers on the right. So?
17
64 reads
CURATED FROM
IDEAS CURATED BY
IN GOD WE TRUST I am free not because i have choices, but i am free because i rely on God with quality assured
Beware of Illusion in Math | Denial of CH Determines that We are not Living On Discrete World
“
The idea is part of this collection:
Learn more about scienceandnature with this collection
The historical significance of urban centers
The impact of cultural and technological advances
The role of urban centers in shaping society
Related collections
Similar ideas to Second Analysis
Getting Technical
In a number set 0 to 99
11% of the numbers start with 1. Likewise, with every other digit from 2 to 9.
In a number set 0 to 199
more than 50% of the numbers start with 1 and less than 6% start with 2 to 9.
In a number set 0 to 299
10 tactics that strengthen your negotiation skills
- Left at the altar - This tactic often yields 11th-hour concessions.
- Making balloon futures - A service is forecasted to be worth more before it's performed.
- Calling a higher authority.
- Crunch time - Where the other party applies pressure.
How To Create Rooms In a Memory Palace
- Bring to mind a room that you are very familiar with.
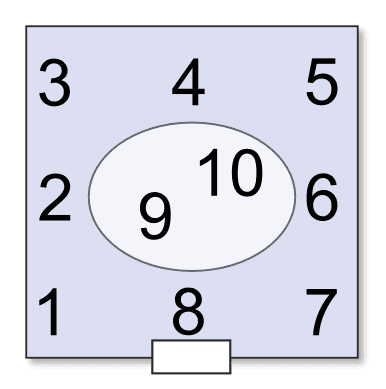
- As you walk into the room you’re familiar with, the corner over your left shoulder is number 1. Then, moving clockwise round the room, the next wall is number 2. And so on, so that there are 8 numbers. 9 will be...
Read & Learn
20x Faster
without
deepstash
with
deepstash
with
deepstash
Personalized microlearning
—
100+ Learning Journeys
—
Access to 200,000+ ideas
—
Access to the mobile app
—
Unlimited idea saving
—
—
Unlimited history
—
—
Unlimited listening to ideas
—
—
Downloading & offline access
—
—
Supercharge your mind with one idea per day
Enter your email and spend 1 minute every day to learn something new.
I agree to receive email updates