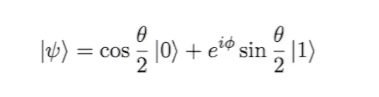Quantum Logic Gates
Curated from: studentsxstudents.com
Ideas, facts & insights covering these topics:
13 ideas
·967 reads
9
Explore the World's Best Ideas
Join today and uncover 100+ curated journeys from 50+ topics. Unlock access to our mobile app with extensive features.
BITS And LOGIC GATES
If you know a bit about computers, you may know that computers use bits, which can either be on or off, usually referred to as 1 and 0 respectively. The states of these bits can be modified using logic gates like AND, OR, XOR , etc. Quantum computers also have bits and logic gates, though they get a bit more complicated.
12
145 reads
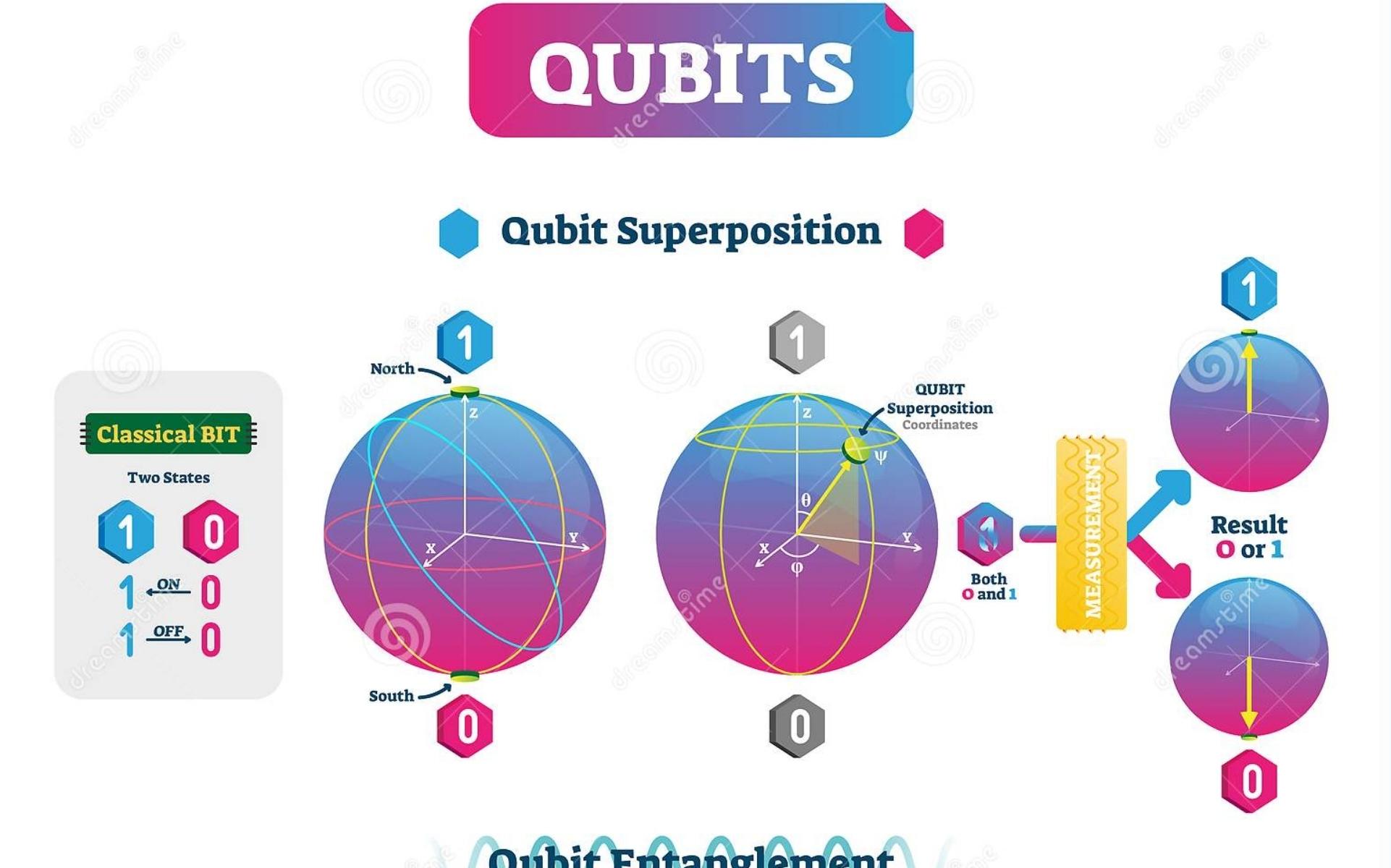
Qubits
Qubits are the quantum equivalent of bits, but they work very differently from classical bits (the bits used in our computers). Qubits, like classical bits, can be in states of 0 and 1, also known as spin up and spin down, but what makes qubits useful is the concept of quantum superposition.
12
128 reads
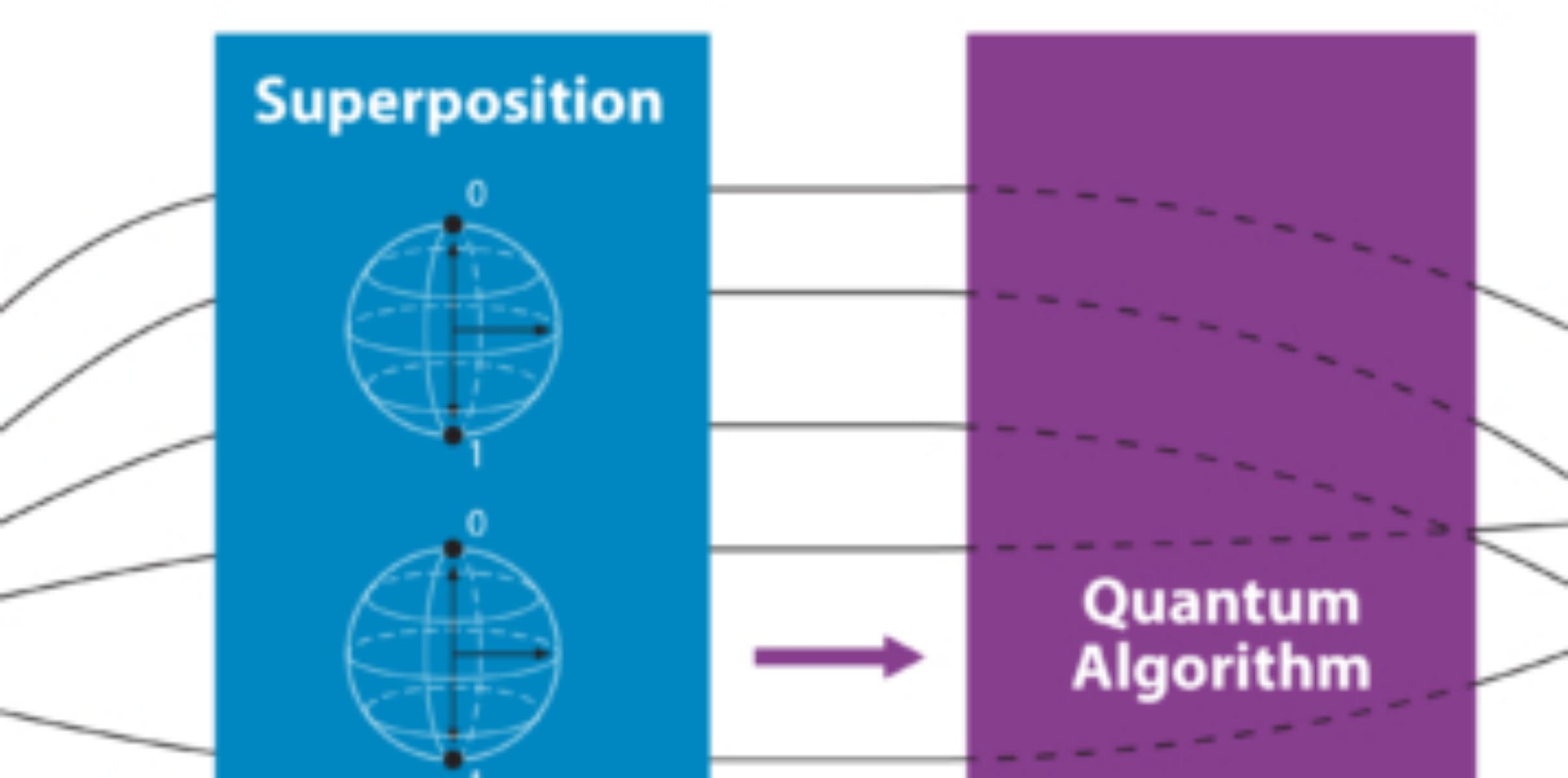
Superposition
In Brief,
Superposition is essentially when a qubit is in a state somewhere in between 0 and 1 that then becomes either 0 or 1 when observed. A very common example is one of a spinning coin. When you flip a coin, there is a mixture of heads and tails (like a qubit being in the states of 0 and 1) but when it stops, it is either heads or tails (this is what happens when we observe the qubit to get the result of our calculation).
Calculations can be performed while the qubit is in a superposition, which is what makes quantum computers so powerful.
13
92 reads
Now some math
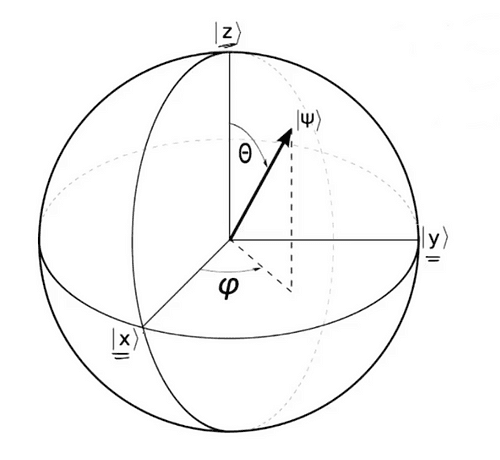
Qubits can be represented using an equation, which is what we will do.
This equation is very useful when working with the Bloch sphere, which is a great tool for visualizing the state of a qubit.
Now let me explain what is going on. The |0> and |1> are just the states of 0 and 1, using a notation commonly used in quantum equations called the bra-ket notation. e is Euler’s number and i is the imaginary unit .
11
99 reads
Introduction
For this article, you won’t need to worry too much about these. Just know that they are important when representing the states of the qubit because a lot of quantum mechanics uses imaginary numbers.The theta and phi symbols are used to describe a vector on the Bloch sphere. In quantum mechanics, the theta influences the magnitude and phi determines the phase of the qubit. Again, you don’t need to understand this terminology for the purposes of this article as they can be thought of as angles on the Bloch sphere but I will link more information at the end of the article.
12
73 reads
Finally, for the Bloch sphere
You’ve heard a bunch about this Bloch sphere throughout this article and it is just a sphere that is used to visualize the state of a qubit. So how does any of this relate to qubit logic gates? Well, logic gates correspond to rotations on the Bloch sphere, which modify the equation previously mentioned.
Each gate also corresponds to a transformation matrix, but I won’t be talking about that in this article.
As you can see both theta and phi correspond to angles.
11
75 reads
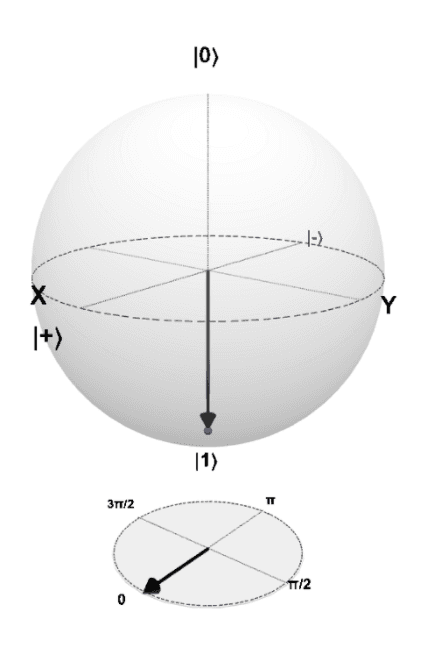
Depiction
This is the Bloch sphere in the 0 state. Both theta and phi are at 0 right now.
cos(0/2) = 1
sin(0/2) = 0
This means that there is a 100% chance that this qubit is in the state of 0.
This is generally the starting state of qubits when it comes to quantum computing.
The gray circle at the bottom corresponds to phi.
A gate will cause the vector (the arrow in this case) to rotate in a certain way
11
64 reads
The phase
One important thing to remember when it comes to the Bloch sphere and quantum gates is the phase of the qubit. The phase will generally “point” in the same direction as the arrow. If we look at the equation, phi is the angle of the arrow on the 2D (x and y axes) plane. The phase is very important in quantum computing but it is a separate subject altogether, so I will link more resources at the bottom.
So now let’s look at some common gates.
11
48 reads
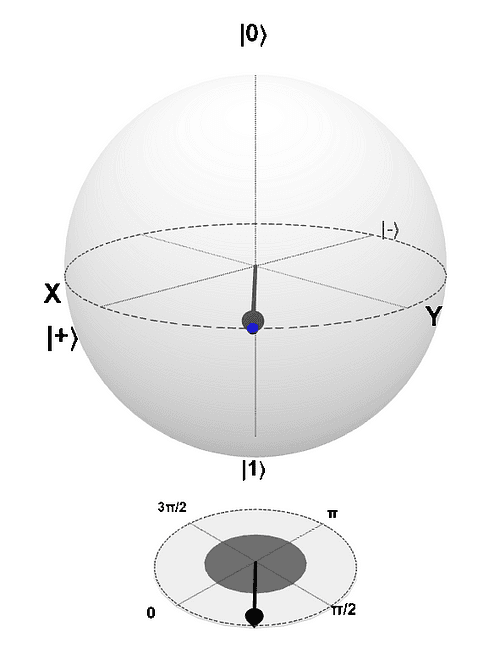
The Pauli-X And Pauli-Y Gates
First we will look at the Pauli-X gate,also known as the NOT gate,and works very similarly to the NOT gate in classical computer science.All it does is switch the probabilities of |0>and |1>. So if we start the qubit with a 100%possibility of being0,then this gate will change it to a 100% possibility of being in the 1 state.
This is how the Blochsphere representation of the qubit will look if the NOTgate was applied on the previously shown gate of 0.
Notice the 180degree rotation around thex-axis.
The Pauli-Ygate corresponds to a 180degree rotation around they-axis,similar to thePauli-Xgate
11
50 reads
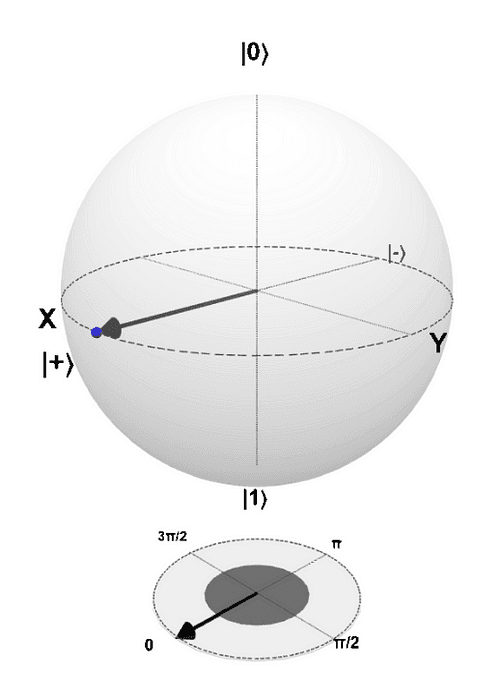
The Hadamard Gate
The Hadamard gate is very important because it puts the qubit into a state of superposition. It corresponds to a 90-degree rotation around the x and the z axes.
After applying the Hadamard gate you are in between the 0 and 1 states, meaning there is a 50% chance that the qubit will result in a 0 and a 50% chance that the qubit results in a 1.
There are in-between states. For example, 25% chance for 0 and 75% chance for 1.
11
49 reads
The T, S and Pauli-Z Gates
These three gates correspond to rotations around the z-axis by different amounts, with T being a 45-degree rotation, S being a 90-degree rotation and Pauli-Z being a 180-degree rotation.
The T gate was applied after a Hadamard gate.
The T gate changed the phase to π/4
11
51 reads
In Continuation...
The Z gate was applied after a Hadamard gate.
The Z gate changed the phase to π
The T and S gates both have inverse gates that correspond to a rotation in the opposite direction. For example, if the inverse of the S gate was applied after a Hadamard gate, the phase would be 3π/2. The Pauli-Z gate does not have an inverse because applying it twice brings it back to the original position. (180-degrees + 180-degrees = 360-degrees which is a full rotation)
11
45 reads
Conclusion
I hope that this article was a nice introduction to quantum gates and some of the math behind it. There are many things I could not mention or explain in this article for the sake of time and staying on-topic but this is the groundwork to start learning more concepts.
11
48 reads
IDEAS CURATED BY
卐 || एकं सत विप्रा बहुधा वदन्ति || Enthusiast || Collection Of Some Best Reads || Decentralizing...
अर्हम् Arham's ideas are part of this journey:
Learn more about personaldevelopment with this collection
How to make sustainable choices in everyday life
Identifying ways to reduce waste and conserve resources
Understanding the impact of human actions on the environment
Related collections
Similar ideas
14 ideas
Your Guide to Quantum Algorithms
medium.com
2 ideas
What is a quantum computer?
newscientist.com
16 ideas
What is a Quantum Convolutional Neural Network?
analyticsindiamag.com
Read & Learn
20x Faster
without
deepstash
with
deepstash
with
deepstash
Personalized microlearning
—
100+ Learning Journeys
—
Access to 200,000+ ideas
—
Access to the mobile app
—
Unlimited idea saving
—
—
Unlimited history
—
—
Unlimited listening to ideas
—
—
Downloading & offline access
—
—
Supercharge your mind with one idea per day
Enter your email and spend 1 minute every day to learn something new.
I agree to receive email updates