Brahmagupta’s Contributions in Mathematics – StudiousGuy
Curated from: studiousguy.com
Ideas, facts & insights covering these topics:
25 ideas
·400 reads
1
Explore the World's Best Ideas
Join today and uncover 100+ curated journeys from 50+ topics. Unlock access to our mobile app with extensive features.
13. Brahmagupta Acharya
He was a great mathematician and astronomer. Brahamgupta considered himself to be an astrologer, maybe because his father Jisnugupta was an astrologer but today, he is mostly remembered for his significant works in the field of mathematics. He was born in 598 CE in Bhinmal, a city in Rajasthan. He spent a major part of his life in Rajasthan. Ujjain was the centre of Indian mathematical astronomy in ancient times and Brahamgupta was the director of this centre. While he was in Ujjain, he wrote many books on mathematics and astronomy.
6
56 reads
These include
‘Durkeamynarda’ (672), ‘Khandakhadyaka’ (665), ‘Brahmasphutasiddhanta’ (628) and ‘Cadamakela’ (624). The ‘Brahmasphutasiddhanta’ meaning the ‘Doctrine of Brahamagupta’ is one of his well-known works. The ‘Brahmasphutasiddhanta’ consists of 25 chapters. In the first 10 chapters, topics covered are, mean longitudes of the planets, true longitudes of the planets, the three problems of diurnal rotation, lunar eclipses, solar eclipses, risings and settings, the moon’s crescent, the moon’s shadow, conjunctions of the planets with each other,
5
37 reads
...
and conjunctions of the planets with the fixed stars. The rest of the 15 chapters are focused more on mathematical concepts. One of his fellow mathematicians gave him the title of ‘Ganita Chakra Chudamani’ which when translated meant, ‘The gem of the circle of mathematicians’. It is believed, that he died in Ujjain, in 668 CE. His contributions to mathematics are mentioned below.
5
24 reads
1.Properties Of Zero
According to him,zero is a number that is obtained, when a number is subtracted from itself. He also mentioned some properties of zero, where positive numbers are termed as fortunes and negative numbers are termed as debt.
- When zero is added to a number or subtracted from a number, the number remains unchanged; and a number multiplied by zero becomes zero.
- A debt minus zero is a debt.
- A fortune minus zero is a fortune.
- Zero minus zero is a zero.
- A debt subtracted from zero is a fortune.
- A fortune subtracted from zero is a debt.
- The product of zero multiplied by a debt or fortune is zero.
5
35 reads
...
- The product of zero multiplied by zero is zero.
- The product or quotient of two fortunes is one fortune.
- The product or quotient of two debts is one fortune.
- The product or quotient of a debt and a fortune is a debt.
- The product or quotient of a fortune and a debt is a debt.
- His some conclusions on the division by zero.
"Positive or negative numbers when divided by zero is a fraction with zero as denominator. Zero divided by negative or positive numbers is either zero or is expressed as a fraction with zero as numerator and the finite quantity as denominator. Zero divided by zero is zero.”
5
28 reads
2. Brahmagupta’s Method of Multiplication
He proposed a method of multiplication, “gomutrika”, in his book “Brahmasphutasiddhanta”. The title of this method was translated by Ifrah as, “Like the trajectory of cow’s urine”. In the 12th chapter of his book, he also tried to explain the rules of simplifying five types of combinations of fractions:-
ac + bc; ac × bd; a1 + bd; ac + bd × ac = a(d + b)cd; and ac − bd × ac = a(d − b)cd.
Let us try to multiply 315 by 306 with the help of the gomutrika method in the Link Attached above.
6
30 reads
3. Intermediate Equation
proposed some methods to solve equations of the type ax + by = c. According to Majumdar, Brahmgupta used continued fractions to solve such equations. He also tried to solve quadratic equations of the type ax² + c = y² and ax² – c = y². For example, for the equation 8x² + 1 = y² he obtained the solutions as (x, y)= (1, 3), (6, 17), (35, 99), (204, 577), (1189, 3363),..He also solved 61x² + 1 = y² having solution as x = 226153980, y = 1766319049 as its smallest solution.
5
18 reads
A sample of the types of problem solved by him is:-
"Five hundred drammas were loaned at an unknown rate of interest, The interest on the money for four months was loaned to another at the same rate of interest and amounted in ten mounths to 78 drammas. Give the rate of interest.”
5
21 reads
4. Sum Of Series
the sum of, a series of cubes and a series of squares for the first n natural numbers as follows:
1² + 2² +…….+n² = (n)(n+1)(2n+1)⁄6
1³ + 2³ +…….+n³ = (n(n+1)⁄2)²
5
18 reads
5. Pythagorean Triplets
Brahmagupta in chapter 12, entitled “Calculation”, of his book, proposed a formula that was useful in generating Pythagorean triplets. He mentioned,
The height of a mountain multiplied by a given multiplier is the distance to a city; it is not erased. When it is divided by the multiplier increased by two it is the leap of one of the two who make the same journey.”
6
17 reads
6. Pell’s Equation
Brahmagupta studied this equation 1000 years before Pell’s birth. Pell’s equation is of form, nx² + 1 = y², which can also be written as y² – nx² = 1, where ‘n’ is an integer and we have to solve it for (x, y) integer solutions. Brahmagupta also provided a lemma, in which he stated that if (a, b) and (c, d)
are integer solutions of ‘Pell type equations’ of the form na²+ k = b² and nc² + k’ = d²
then, (bc + ad, bd + nac) and (bc – ad, bd – nac)are both integer solutions of the ‘Pell type equation’.
5
16 reads
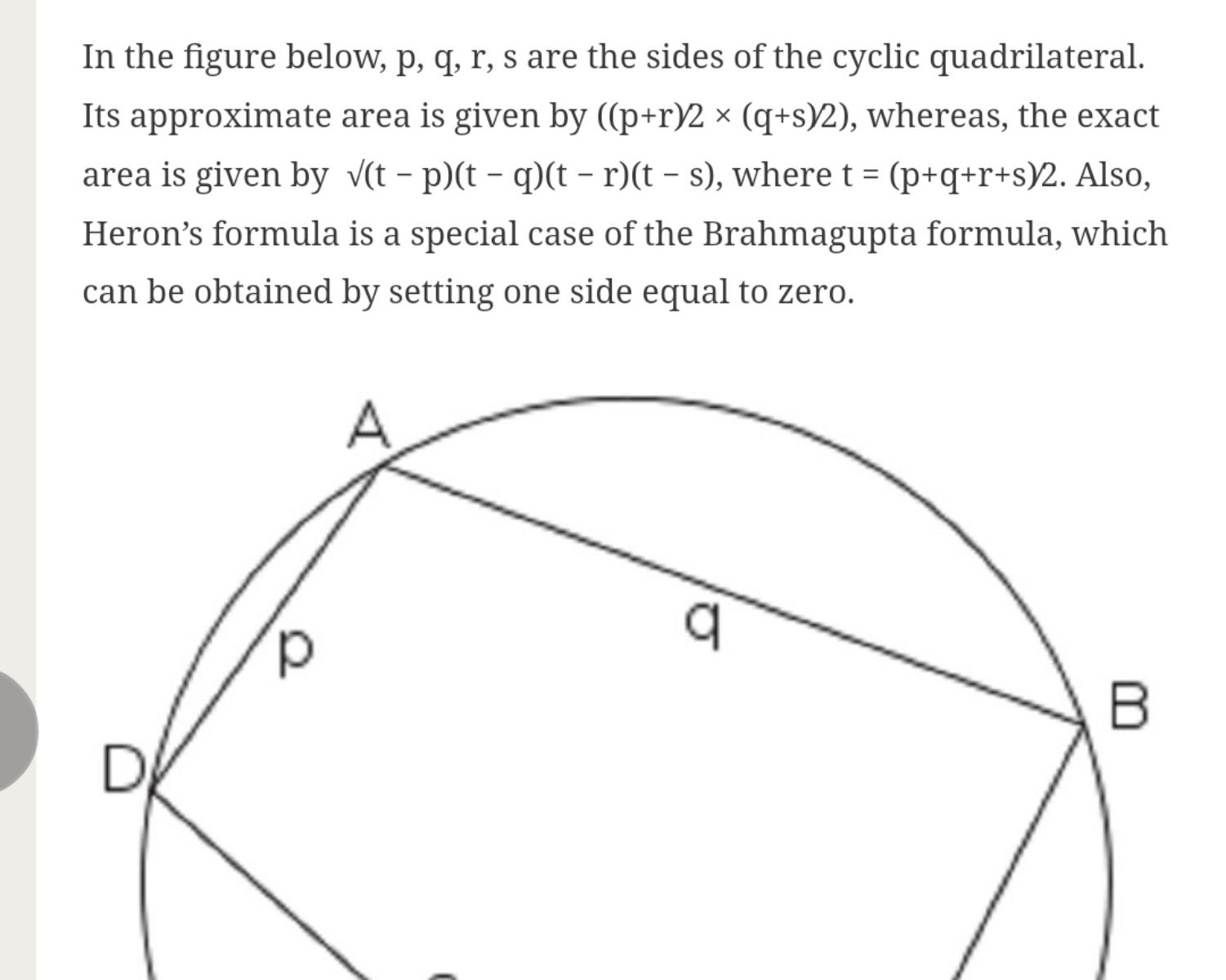
7. Brahmagupta 'S Formula
Brahmagupta’s formula for the cyclic quadrilaterals is regarded as his most famous discovery in geometry. Given the sides of a cyclic quadrilateral, he provided an approximate and exact formula for the area of the cyclic quadrilateral. He mentioned,
"The approximate area is the product of the halves of the sums of the sides and opposite sides of a triangle and a quadrilateral. The accurate area is the square root from the product of the halves of the sums of the sides diminished by each side of the quadrilateral.”
5
10 reads
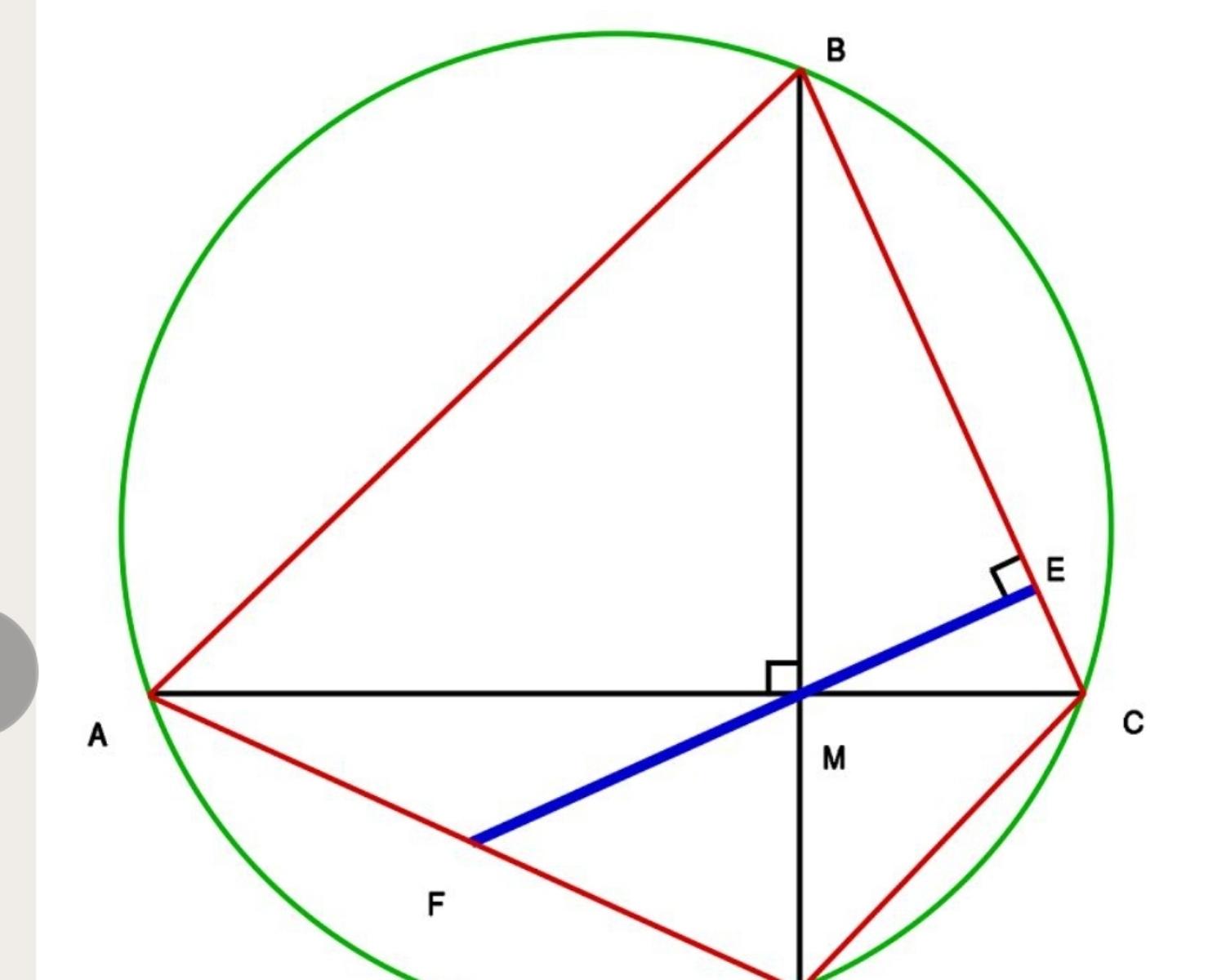
8. Brahmagupta’s Theorem
Brahmagupta theorem states that,
If a cyclic quadrilateral is orthodiagonal (i.e., has perpendicular diagonals), then the perpendicular to a side from the point of intersection of the diagonals always bisects the opposite side.”
Geometrically, this theorem means that, in a cyclic quadrilateral ABCD, diagonals AC and BD are perpendicular to each other. The intersection of AC and BD is M. Drop the perpendicular from M to the line BC, calling the intersection point E. Let F be the intersection of the line EM and the side AD. Then, according to the theorem, F is the midpoint of side AD.
5
7 reads
...
Brahmagupta further extended his theory and claimed that, The square-root of the sum of the two products of the sides and opposite sides of a non-unequal quadrilateral is the diagonal. The square of the diagonal is diminished by the square of half the sum of the base and the top; the square-root is the perpendicular altitudes.”
The above statement means that in an isosceles trapezoid having sides of length p, q, r, s, the length of the diagonal is given by √pr+qs.
5
12 reads
9. Triangles
A major portion of Brahmagupta’s work was dedicated to the study of geometry. One of his theorem about triangles states that,
The base decreased and increased by the difference between the squares of the sides divided by the base; when divided by two they are the true segments. The perpendicular altitude is the square-root from the square of a side diminished by the square of its segment.”
This theorem gives the length of two segments in which the base of a triangle is divided by its altitude, and the lengths are, 12(b ± (c2 − a2)
5
8 reads
...
He also discussed rational triangles. A rational triangle with the rational area and sides a, b, c, are of the form:
a = 1⁄2(u²⁄v + v), b = 1⁄2(u²⁄w + w), c = 1⁄2(u²⁄v – v + u²⁄w – w), for some rational numbers u, v, w.
5
8 reads
10. Approximation of π
Brahmagupta also tried to approximate the value of π and in stanza 40 of his book he mentioned,
The diameter and the square of the radius, each multiplied by 3 are the practical circumference and the area of a circle respectively. The accurate values are the square-roots from the squares of those two multiplied by ten.”
He used √10 ≈ 3.1622….. approximated to 3, as an accurate value of π with an error of less than 1%.
5
8 reads
11. Measuration And Construction
Brahmagupta illustrated the construction of several figures with arbitrary sides. He tried to construct figures such as isosceles triangles, scalene triangles, rectangles, isosceles trapezoids, isosceles trapezoids with three equal sides, and scalene cyclic quadrilateral, mainly, with the help of right triangles. He also gave the volume and surface area of some figures, after estimating the value of π. He found the volume of rectangular prisms, pyramids and frustum of a square pyramid. He further proposed the average depth of a series of pits.
5
6 reads
12. Trigonometry
Brahmagupta in his chapter 2 of his book, provided a sine table. He wrote,
The sines: The Progenitors, twins, Ursa Major, the Vedas, the gods, fires, flavors, dice, the moon, the sky, the moon, arrows, sun…..”
He used the above objects to represent digits of place-value numerals. Progenitors represent 14 progenitors in Indian cosmology, twins means 2, Ursa Major represents the seven stars of Ursa Major or 7, Vedas refers to the 4 Vedas or 4, dice represents the number of sides of the traditional die or 6, and so on. He gave the sine table with 3270 as radius and calculated 3270 sin(π⁄48).
5
6 reads
13. Interpolation Method
He was the first who propose an interpolation formula using second-order difference. His Sanskrit verses on this formula were found in the Khandakadyaka work of Brahmagupta. Today, the Brahmagupta interpolation formula is known as Newton- Stirling interpolation formula. In his book, he termed the difference Dr as the ‘gatakhanda’, the difference Dr+1 as the ‘bhogyakhanda’, ‘Vikala’ as the quantity in minutes by which the interval has been covered at the point of interpolation, which in modern notation denoted as a− xr. ‘Sphuta-bhogyakhanda’ is now known as fr+1 − fr.
5
6 reads
Sphuta-bhogyakhanda
A formula stated by him, for the computation of values of the sine table, having common interval (h) in the underlying base table as 900 minutes or 15 degrees, is given below.
When translated these verses means,
Multiply the ‘vikala’ by the half the difference of the ‘gatakhanda’ and the ‘bhogyakhanda’ and divide the product by 900. Add the result to half the sum of the ‘gatakhanda’ and the ‘bhogyakhanda’ if their half-sum is less than the ‘bhogyakhanda’, subtract if greater. The result in each case is ‘sphuta-bhogyakhanda’ the correct tabular difference.
5
6 reads
...
In modern notation, the formula is denoted as sphuta-bhogyakhanda = (Dr + Dr-1)⁄2 ± t|Dr – Dr-1|⁄2, where ± is introduced according to Dr
5
5 reads
14. Algebra
Brahmagupta gave the solution of general linear equations in chapter 18 of his book and wrote,The difference between rupas, when inverted and divided by the difference of the coefficients of the unknowns, is the unknown in the equation. The rupas are subtracted on the side below that from which the square and the unknown are to be subtracted.”
Algebraically, the above statement means that, for an equation of type bx+c = dx+e, the solution is given by x = e − c/b − d. He also gave two solutions for the quadratic equation ax² +bx = c, and wrote,
5
6 reads
...
Diminish by the middle number the square-root of the rupas multiplied by four times the square and increased by the square of the middle number; divide the remainder by twice the square.”
By this method, the solution is given by, x = ±(√(4ac+b²) – b)⁄2a. Whatever is the square-root of the rupas multiplied by the square and increased by the square of half the unknown, diminished that by half the unknown and divide the remainder by its square. The result is the unknown.”By this method, the solution is given by, x = ±(√(ac+b²⁄4) – b²⁄2)⁄a.
5
6 reads
Ganita Chakra Chudamani Brahmagupta
Although Brahmagupta thought of himself as an astronomer who did some mathematics, he is now mainly remembered for his contributions to mathematics. He was honoured by the title given to him by a fellow scientist ‘Ganita Chakra Chudamani’ which is translated as ‘The gem of the circle of mathematicians’.
5
6 reads
IDEAS CURATED BY
卐 || एकं सत विप्रा बहुधा वदन्ति || Enthusiast || Collection Of Some Best Reads || Decentralizing...
अर्हम् Arham's ideas are part of this journey:
Learn more about education with this collection
Basic survival skills
How to prioritize needs in survival situations
How to adapt to extreme situations
Related collections
Similar ideas
2 ideas
Introduction to Matrices | Boundless Algebra
courses.lumenlearning.com
4 ideas
Why Mathematics Is a Language
thoughtco.com
17 ideas
A BUTTERFLY IN THE QUANTUM WORLD
canblogum.medium.com
Read & Learn
20x Faster
without
deepstash
with
deepstash
with
deepstash
Personalized microlearning
—
100+ Learning Journeys
—
Access to 200,000+ ideas
—
Access to the mobile app
—
Unlimited idea saving
—
—
Unlimited history
—
—
Unlimited listening to ideas
—
—
Downloading & offline access
—
—
Supercharge your mind with one idea per day
Enter your email and spend 1 minute every day to learn something new.
I agree to receive email updates