A BUTTERFLY IN THE QUANTUM WORLD

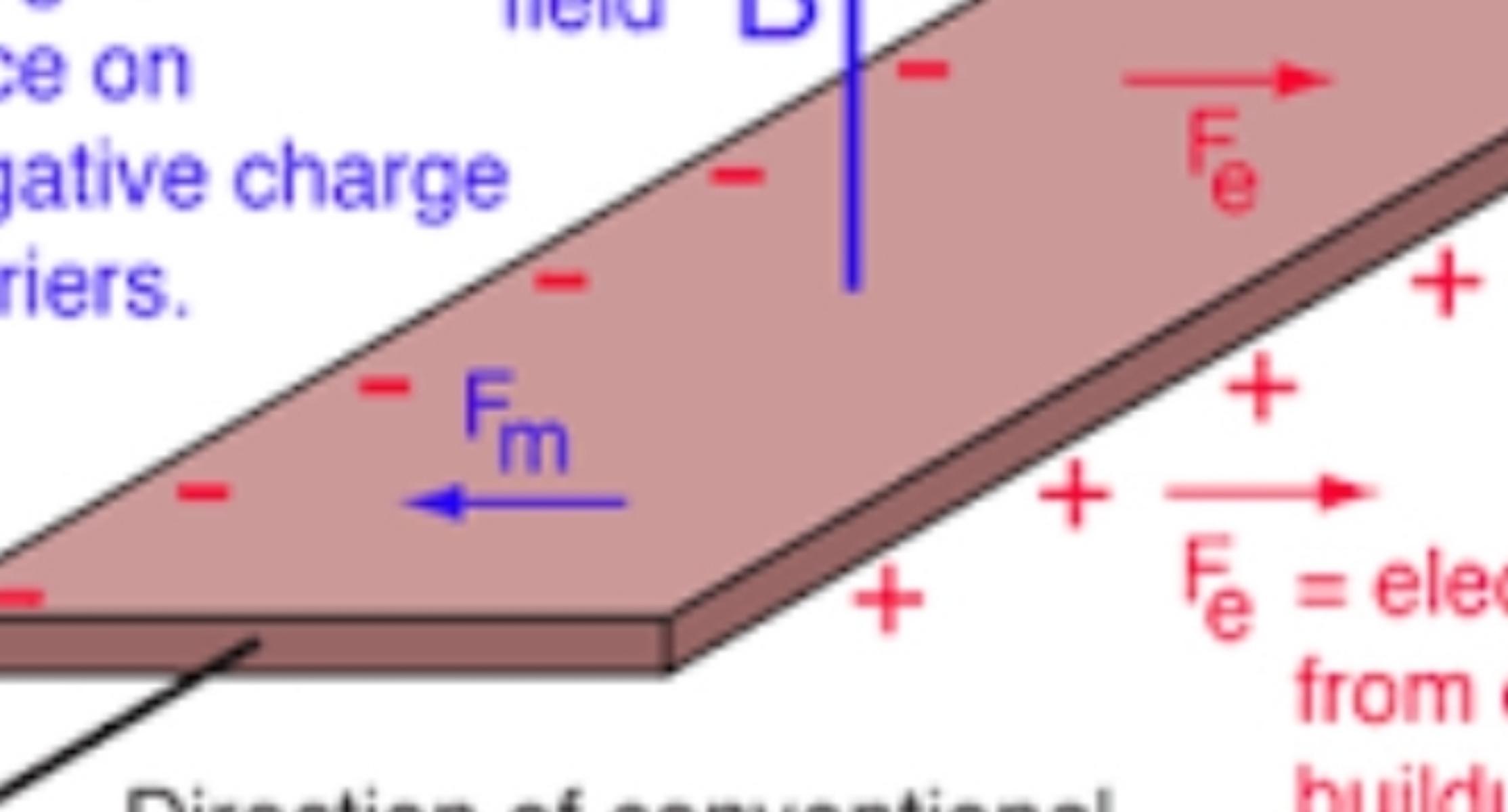
A one of the most interesting phenomena (Hall voltage) in physics was first observed by Edwin Hall in 1879. Let’s imagine that we have a horizontal conductive plate(Hall element)and with the help of any power source we supply current to the plate in a particular direction. So we will have electrons carrying current along a straight line on the plate.

Now,apply external magnetic field perpendicular to the plate.Since the magnetic field exerts a magnetic force(Lorentz force) on a charged particle,the moving electrons and the protons will move towards the edges of the plate in opposite directions.

Potential difference is required for the existence of voltage in a particular direction. In our experiment, electrons and protons stacked on opposite sides to create a potential difference perpendicular to the current. This voltage is called the Hall voltage . Also, this phenomena is called the classical Hall effect.

The version of the Hall effect in the subatomic world is called the quantum Hall effect. We should expect to observe the classic Hall effect at low magnetic field, room temperature and at very high magnetic fields (about 10 Tesla) , very low temperatures (about 100 Kelvin) expect to observe the quantum Hall effect.

The main difficult problem, which is the main theme of the article, is rather than explaining the classical Hall effect to be able to explain what happens to an electron that can move forward withoutscattering in the presence of a magnetic field.

In quantum mechanics, classically forbidden phenomena are likely to occur. For any particle to pass over a potential barrier , it needs energy . If the energy of a particle is lower than the potential barrier , the particle is trapped there. In other words, it is not possible for the particle to pass over the barrier in the classical sense. But quantum mechanics says that even in such a case there is a possibility that the particle is outside the potential barrier . We’re talking about a kind of particle teleportation .

The main reason why we don’t think of teleportation as a spontaneous natural event is that it never happens in daily life (by the laws of classical mechanics). Because the wavelength of the wave (or particle) much less than the width of the barrier . This also decreases the probability . That’s why you can never teleport to the other side of the wall, even if you wait your whole life with your hand on the wall.

In the quantum mechanics, every particle is also a wave . As we know from daily life, light waves (photon particles) scatter as they pass through raindrops and formed a rainbow. We assume that an electron does not undergo such scattering due to its movement in the crystal lattice medium.

Our other most remarkable assumption is the tight-binding approach. According to this approach, electrons can only tunnelling into the nearest neighboring atomic orbitals. Thus, we make our work easier by ignoring interactions with distant neighbors.

Multidimensional lattice, a mathematical structure for molecules, was modeled in condensed matter physics (solid state physics) which is a sub-area of physics to solve the problem. In this model, we can imagine the lattice (can be of any geometry) with atoms in point form at each corner.

In the context of this model, the mathematical equation describing the motion of a single electron living on a two-dimensional square lattice is called the Harper equation . It was studied by Rudolf Peierls andR. G. Harper in the 1950s. There is something that makes the equation very special: the alpha values included in the equation. The striking results of the difference in the number sets (rational or irrational) to which alpha belongs… By definition, the alpha value is the ratio of the quantum flux (a definition in the literature) to the magnetic flux passing through each plate.

Since the ratio will still give the magnetic field unit, the alpha value is the external magnetic field itself. The results will differ depending on whether the value of the external magnetic field is rational or irrational .

Here, the flux can be thought of as magnetic field lines pass through a unit surface and the magnetic flux is proportional to the magnetic field lines passing through the surface.

All that remains in solving the problem is to solve the finite set of Harper equations using numerical solution (computational) techniques. In other words determining the energy values in each of the equations in this finite set. It was solved byDougles R. Hofstadter in 1976.

Now that we have the solutions, let’s look at their dependence on external magnetic field (alpha values) . Let’s consider alpha values a rational number. In other words, the magnetic field that we apply to the system should only be in rational values. In this case, if the energy solutions corresponding to each alpha values

(energy as a function of alpha) are plotted, we will see the Hofstadter Butterfly , which similar to butterfly wings.

Note that the graph is symmetrical with respect to the zero of the energy and alpha = 1/2 value. The symmetry presents us an image similar to the patterns on the wings of a butterfly in nature. Additionally, the larger the set of equations being studied, the butterfly pattern (solutions) will become sharper .

As can be seen from the graphs above, the most important reason why Harper’s equation is to be worked only numerically is that it contains too many points (solutions)

and naturally too many equations.

Let’s take a closer look to see one of the beautiful details of theHofstadter Butterfly . You can clearly see the band separations in the left graph above. It is the number in the denominator of the alpha value that determines how many times the bands will be split . If alpha = 1/3 , we see decompositions into three , and if alpha=9/11 , we see decomposition into eleven and so on... Band corners joins at alpha=1/2 and energy=0 solution, thus we saw single band .

In other words, let’s choose the external magnetic field we apply not rational , but only irrational . What can change, you might say. After all, there is only 0.5 difference between alpha=1/2 and alpha=1 . But that is not the case. The very interesting thing is that the butterfly only occurs for rational alpha values! If we plot the solutions of Harper’s equation corresponding to the irrational values of alpha ; we get nothing more than horizontal arrays of dots !

If we look at the graph below, we see visually sense pointless results for irrational alpha values . But, as we saw in the previous graph,Hofstadter Butterflies lives in the white regions (range of rational values) of the graph below.

Just as different types of butterflies exist in nature, the Hofstadter Butterfly is not unique in physics. Naturally, fractal patterns will be different in systems that exhibit different behaviors under different types of features. Above, we only talked about two-dimensional square lattice model solutions. For example, if we analyzed hexagonal (honeycomb) or triangular lattice structures using similar numerical methods under a magnetic field, we would get different graphs. Just like bent, twisted and modified versions of the Hofstadter Butterfly.