Variance-Invariance-Covariance Regularization for Self-Supervised Learning
Curated from: arxiv.org
Ideas, facts & insights covering these topics:
3 ideas
·130 reads
5
Explore the World's Best Ideas
Join today and uncover 100+ curated journeys from 50+ topics. Unlock access to our mobile app with extensive features.
Self-Supervised Learning
Labelled data is expensive, which makes benefiting from the current success in supervised learning unfeasible for smaller companies.
However, good representations can be learned without any task-specific information from raw data.
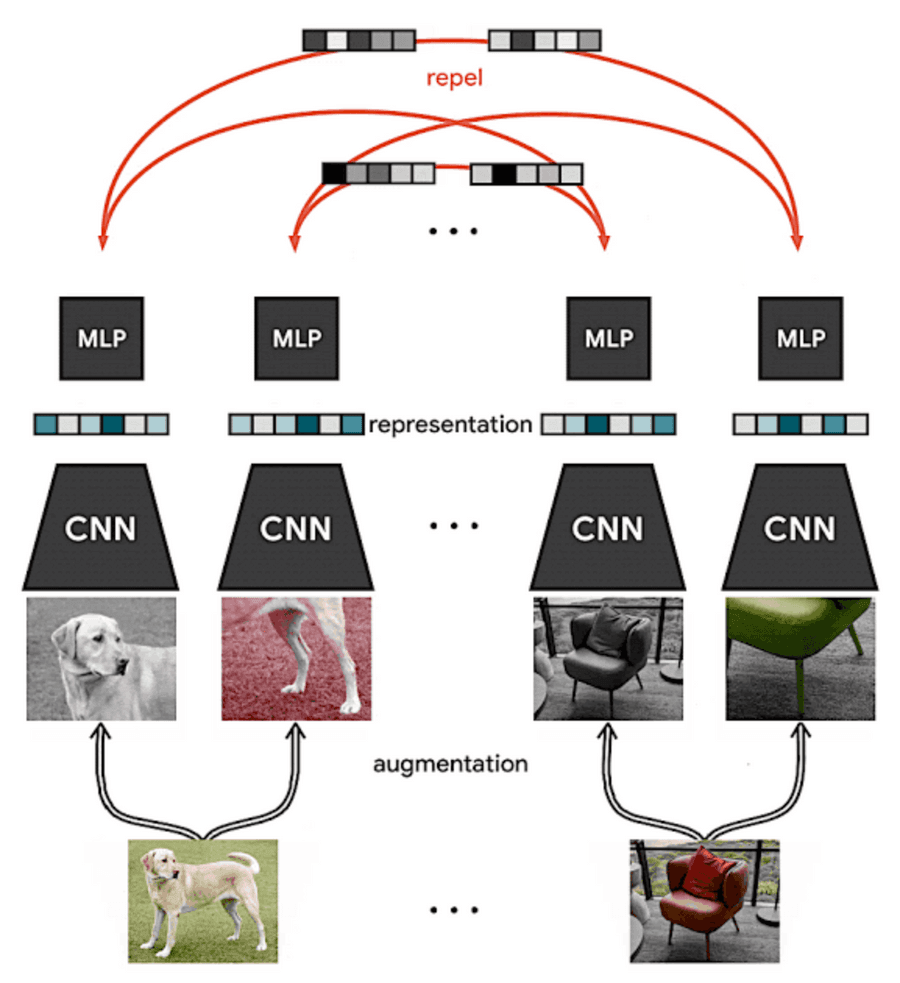
In self-supervised learning, labels are generated artificially. A common approach is to take multiple augmented views from the same source and contrast them to different sources.
Many papers have proven that simply increasing the similarity (decreasing the distance in the embedding space) of such views from the same source can lead to strong representations.
7
66 reads
Quality of Representations
Good representations are expressive and make efficient use of the given dimensionality.
We want the representations to be variant to contextual changes that are essential to a task and invariant to changes related to factors that we cannot control nor care about.
While these invariances can largely be enforced through task-specific data augmentation, the efficient use of the dimensionality of the representations has to be achieved through clever algorithms.
One way to look at this quality is through the variance of the representations, which shall not collapse for a given class of inputs.
7
37 reads
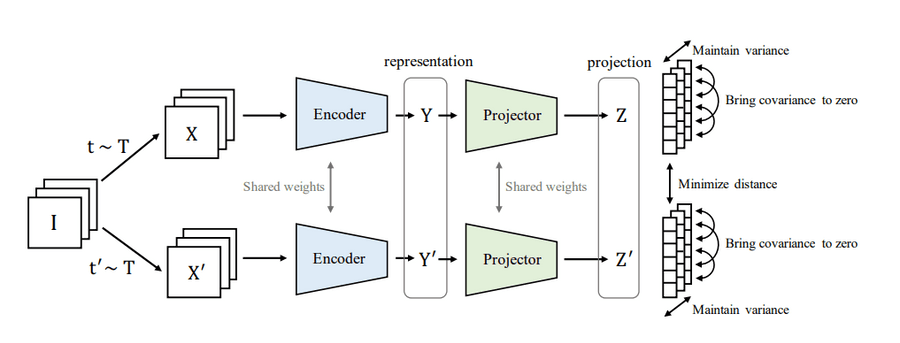
VICReg
While many recently proposed self-supervised learning algorithms prevent a collapse of the embedding-space implicitly through various methods like contrasting samples in a batch [SimCLR] or clustering [SwAV], VICReg explicitly regularizes the embedding-space with three terms:
- The Variance of the embeddings should be above a given threshold.
- Euclidian distance between embeddings of different views of the same image enforces Invariance to given augmentations.
- Minimizing the Covariance of the embeddings decorrelates the components, thus efficiently making use of the given space.
7
27 reads
IDEAS CURATED BY
Laurenz 's ideas are part of this journey:
Learn more about artificialintelligence with this collection
The historical significance of urban centers
The impact of cultural and technological advances
The role of urban centers in shaping society
Related collections
Similar ideas
Read & Learn
20x Faster
without
deepstash
with
deepstash
with
deepstash
Personalized microlearning
—
100+ Learning Journeys
—
Access to 200,000+ ideas
—
Access to the mobile app
—
Unlimited idea saving
—
—
Unlimited history
—
—
Unlimited listening to ideas
—
—
Downloading & offline access
—
—
Supercharge your mind with one idea per day
Enter your email and spend 1 minute every day to learn something new.
I agree to receive email updates