Explore the World's Best Ideas
Join today and uncover 100+ curated journeys from 50+ topics. Unlock access to our mobile app with extensive features.
Used in Statistical Models
Parameters of a probability distribution, such as the mean and standard deviation of a normal distribution
Regression coefficients of a regression model, such as Y=a'X
14
218 reads
Used in Dynamic Models
Engineers apply parameter estimation to dynamic models to compute:
Coefficients of transfer functions, including ARX, ARMAX, Box-Jenkins, and output-error models
Entries in state-space matrices
Coefficients of ODEs or well-structured systems with parameter constraints (grey-box system identification).
Regression coefficients, saturation levels, or dead-zone limits for nonlinear dynamic systems, including nonlinear ARX and Hammerstein-Wi.ener
14
136 reads
Types
- Point estimate
- Confidence interval (CI) estimate.
For both continuous variables (e.g., population mean) and dichotomous variables (e.g., population proportion) one first computes the point estimate from a sample.
14
103 reads
Point Estimation
The process of finding an approximate value of some parameter—such as the mean (average)—of a population from random samples of the population.
It is the value of statistic that estimates the value of a parameter.
The sample standard deviation (s) is a point estimate of the population standard deviation (σ).
The sample mean (̄x) is a point estimate of the population mean, μ.
The sample variance (s2) is a point estimate of the population variance (σ2).
14
90 reads
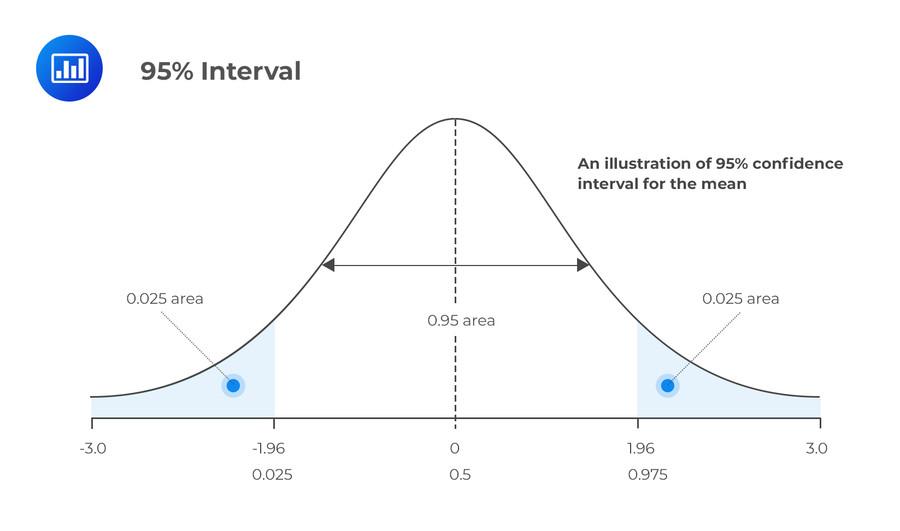
Confidence Interval
Range of values you expect your estimate to fall between if you redo your test, within certain level of confidence.
Confidence-Describes - Probability
Point Estimate +- Margin of error
Given : ( α = 0.05 , n ,x̄ , Population standard deviation σ )
Tests:
- z-test (Population standard is given & n>=30)
- t-test (Population standard is not given & n
14
70 reads
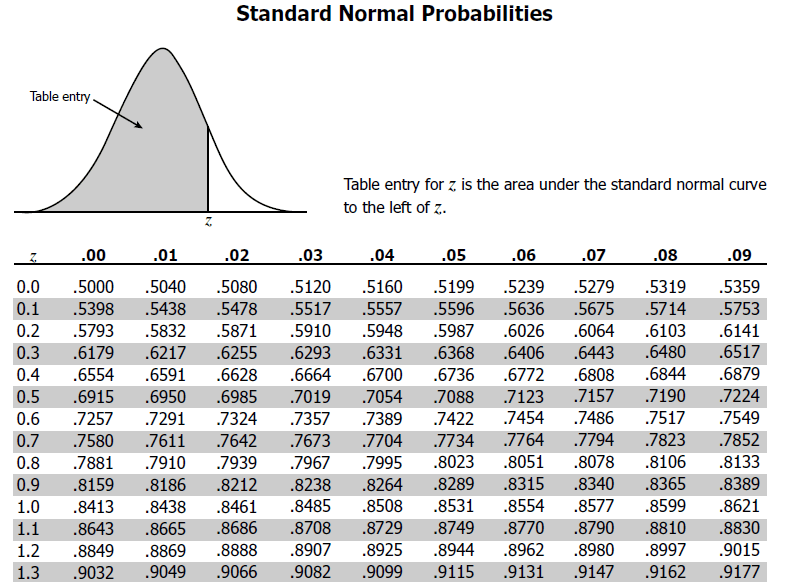
Z-Test - z score
Population standard is given & n >= 30.
Point Estimate +- Margin of error
x̄ +- z α/2 (σ/ √ n )
Upper Bound - x̄ + z α/2 (σ/ √ n ) = ztable(Answer)
Lower Bound - x̄ - z α/2 (σ/ √ n )=ztable(Answer)
14
59 reads
T -test - t-table
Population standard deviation is not given & n >≠ 30.
Point Estimate +- Margin of error
x̄ +- z α/2 (σ/ √ n )
t = degree of freedom= n-1
Upper Bound - x̄ + t α/2 (s/ √ n ) = t table(Answer)
Lower Bound - x̄ - t α/2 (s / √ n )=t table(Answer)
(s / √ n ) is Standard error
14
53 reads
Standard Error
The standard error is the standard deviation of a sample population. It measures the accuracy with which a sample represents a population.
14
55 reads
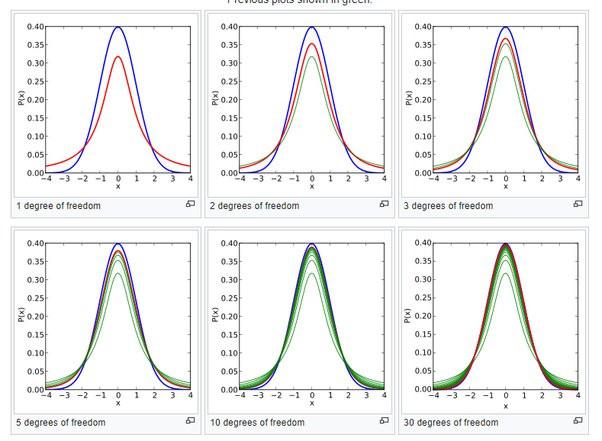
Degree of freedom
Degrees of freedom, often represented by v or df, is the number of independent pieces of information used to calculate a statistic.
It’s calculated as the sample size minus the number of restrictions.
14
57 reads
Suppose you randomly sample 10 American adults and measure their daily calcium intake. You use a one-sample t test to determine whether the mean daily intake of American adults is equal to the recommended amount of 1000 mg.The test statistic, t, has 9 degrees of freedom:
df = n − 1
df = 10 − 1
df = 9
You calculate a t value of 1.41 for the sample, which corresponds to a p value of .19. You report your results:
“The participants’ mean daily calcium intake did not differ from the recommended amount of 1000 mg, t(9) = 1.41, p = 0.19.”
14
56 reads
IDEAS CURATED BY
CURATOR'S NOTE
Parameter estimation is the process of computing a model’s parameter values from measured data. You can apply parameter estimation to different types of mathematical models, including statistical models, parametric dynamic models, and data-based Simulink® models
“
Similar ideas
12 ideas
How to Lie with Statistics
Darrell Huff
7 ideas
Introduction to Statistics for Biomedical Engineers
Kristina M. Ropella
Read & Learn
20x Faster
without
deepstash
with
deepstash
with
deepstash
Personalized microlearning
—
100+ Learning Journeys
—
Access to 200,000+ ideas
—
Access to the mobile app
—
Unlimited idea saving
—
—
Unlimited history
—
—
Unlimited listening to ideas
—
—
Downloading & offline access
—
—
Supercharge your mind with one idea per day
Enter your email and spend 1 minute every day to learn something new.
I agree to receive email updates