How Zeno's Paradox was resolved: by physics, not math alone
Curated from: bigthink.com
Ideas, facts & insights covering these topics:
10 ideas
·1.47K reads
8
1
Explore the World's Best Ideas
Join today and uncover 100+ curated journeys from 50+ topics. Unlock access to our mobile app with extensive features.
Background
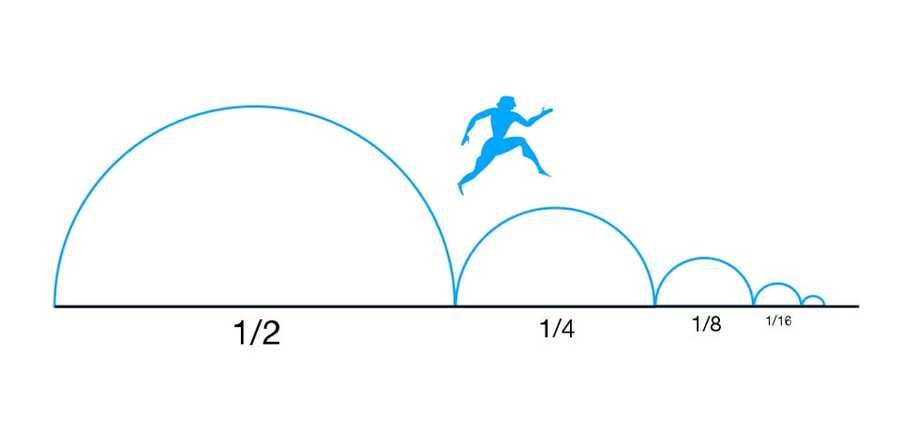
The fastest human in the world, according to the Ancient Greek legend, was the heroine Atalanta.
Although she was a famous huntress who joined Jason and the Argonauts in the search for the golden fleece, she was renowned for her speed. No one could defeat her in a fair footrace.
She was also the inspiration for the first of many similar paradoxes put forth by the ancient philosopher Zeno of Elea about how motion, logically, should be impossible.
10
230 reads
So, What Is Zeno’s Paradox?
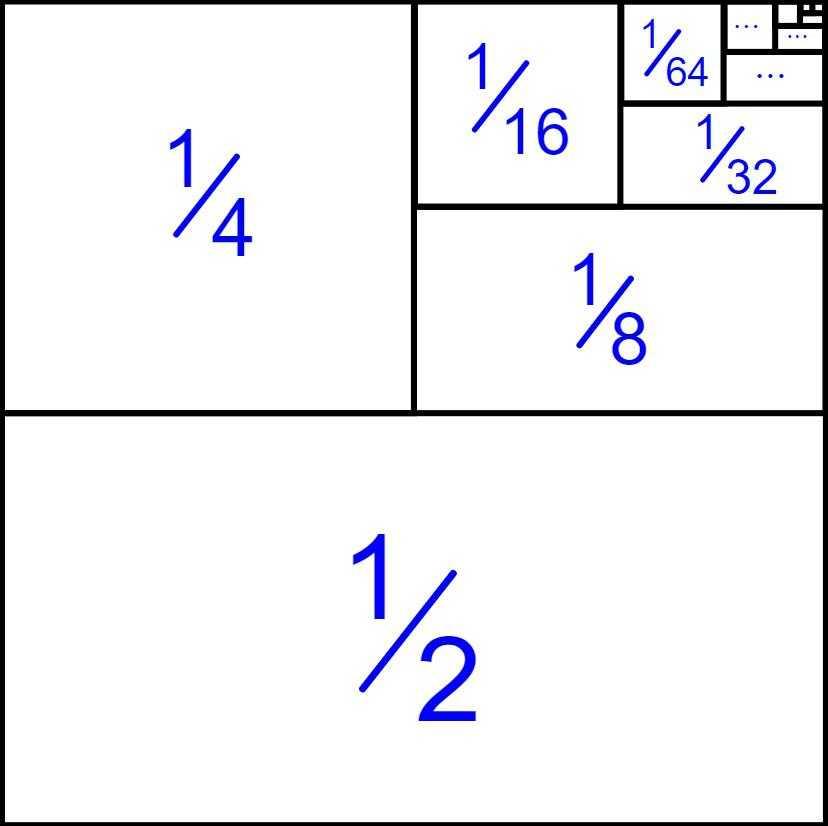
To go from her starting point to her destination, Atalanta must first travel half of the total distance.
To travel the remaining distance, she must first travel half of what’s left over. No matter how small a distance is still left, she must travel half of it, and then half of what’s still remaining, and so on, ad infinitum.
With an infinite number of steps required to get there, clearly she can never complete the journey. And hence, Zeno states, motion is impossible: Zeno’s paradox. Here’s the unintuitive resolution.
10
219 reads
The Initial Solution To The Paradox?
The oldest “solution” to the paradox was done from a purely mathematical perspective. The claim admits that, sure, there might be an infinite number of jumps that you’d need to take, but each new jump gets smaller and smaller than the previous one. Therefore, as long as you could demonstrate that the total sum of every jump you need to take adds up to a finite value, it doesn’t matter how many chunks you divide it into.
Simple, straightforward, and compelling, right?
10
183 reads
Why Is The Initial Solution Flawed?
This reasoning is only good enough to show that the total distance you must travel converges to a finite value. It doesn’t tell you anything about how long it takes to reach your destination.
There's no guarantee that each of the infinite number of jumps you need to take- even to cover a finite distance-occurs in a finite amount of time. If each jump took the same amount of time, for example, regardless of the distance traveled, it would take an infinite amount of time to cover whatever tiny fraction-of-the-journey remains. This way, it is still impossible for Atalanta to reach her destination
10
149 reads
Including The Concept Of Time
Many thinkers, both ancient and contemporary, tried to resolve this paradox by invoking the idea of time.
Specifically, as asserted by Archimedes, it must take less time to complete a smaller distance jump than it does to complete a larger distance jump, and therefore if you travel a finite distance, it must take you only a finite amount of time.
And therefore, if that’s true, Atalanta can finally reach her destination and complete her journey.
9
135 reads
Only, This Is Flawed Too
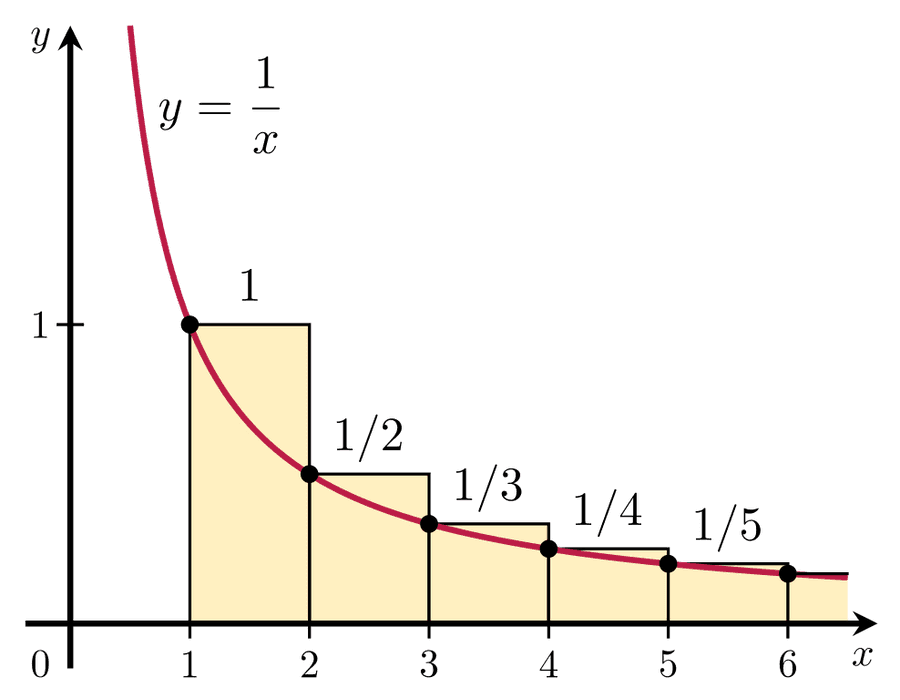
It’s eminently possible that the time it takes to finish each step will still go down: half the original time, a third of the original time, etc, but that the total journey will take an infinite amount of time.
You can check this for yourself by trying to find what the series [½ + ⅓ + ¼ + ⅕ ++ …] sums to. As it turns out, the limit does not exist: this is a diverging series.
Pure mathematics alone cannot provide a satisfactory solution to the paradox, as it isn’t simply about dividing a finite thing up into an infinite number of parts, but rather about the inherently physical concept of a rate
10
117 reads
What Is Velocity?
How fast does something move? That’s a speed.
Add in which direction it’s moving in, and that becomes velocity.
And what’s the quantitative definition of velocity, as it relates to distance and time? It’s the overall change in distance divided by the overall change in time.
10
125 reads
What Then Is Rate?
Rate is the amount that one quantity (distance) changes as another quantity (time) changes as well.
You can have a constant velocity (without acceleration) or a changing velocity (with acceleration).
You can have an instantaneous velocity (your velocity at one specific moment in time) or an average velocity (your velocity over a certain part or whole of a journey).
But if something is in constant motion, the relationship between distance, velocity, and time becomes very simple: distance = velocity * time.
10
100 reads
How Does Rate Provide A Solution
This is the resolution of the classical “Zeno’s paradox” as commonly stated:
The reason objects can move from one location to another (i.e., travel a finite distance) in a finite amount of time is not because their velocities are not only always finite, but because they do not change in time unless acted upon by an outside force.
If you take a person like Atalanta moving at a constant speed, she will cover any distance in an amount of time put forth by the equation that relates distance to velocity.
10
106 reads
Final Thoughts
The takeaway is this:
Motion from one place to another is possible, and because of the explicit physical relationship between distance, velocity and time, we can learn exactly how motion occurs in a quantitative sense.
Yes, in order to cover the full distance from one area to another, you have to first cover half that distance, then half the remaining distance, then half, etc.
But the time it takes to do so also halves, so motion over a finite distance always takes a finite amount of time for any object in motion. This is still an interesting exercise for mathematicians and philosophers.
12
112 reads
IDEAS CURATED BY
CURATOR'S NOTE
I found this paradox is interesting, mainly because it has such a simple solution for what seems like an unsolvable problem.
“
M 's ideas are part of this journey:
Learn more about scienceandnature with this collection
How to choose the right music for different tasks
The benefits of listening to music while working
How music affects productivity
Related collections
Similar ideas
12 ideas
5 Bizarre Paradoxes Of Time Travel Explained
astronomytrek.com
2 ideas
The Physics Behind Schrödinger's Cat Paradox
nationalgeographic.com
5 ideas
Time Travel & the Bootstrap Paradox Explained
astronomytrek.com
Read & Learn
20x Faster
without
deepstash
with
deepstash
with
deepstash
Personalized microlearning
—
100+ Learning Journeys
—
Access to 200,000+ ideas
—
Access to the mobile app
—
Unlimited idea saving
—
—
Unlimited history
—
—
Unlimited listening to ideas
—
—
Downloading & offline access
—
—
Supercharge your mind with one idea per day
Enter your email and spend 1 minute every day to learn something new.
I agree to receive email updates